Mükemmel Paralel Park Etmenin Matematiksel Formülü

Eğer büyük bir şehirde ikamet ediyorsanız bu hikaye sizin de tanıdık gelecektir. Trafik çok kötü! Her daim işe yetişmek için koşturmak durumundayım ve tabii ki tüm otoparklar dolu. Hal böyle olunca sokak aralarında yer arama başlıyoruz. Büyük ihtimal oralarda da pek yer olmuyor ama şansımıza o an yerini terk eden bir araca denk geldiğimiz oluyor zaman zaman. Bu sefer bir diğer problem ortaya çıkıyor, iki aracın arasına park etmek! Eğer bu konuda çok fazla tecrübeniz yoksa o park etmenin stresi daha çalışmaya başlamadan sizi yoruyor.

Üzülmeyin! Geometri dersinde gördüğümüz onca formül ve çözdüğümüz onca soru artık bir işe yarayacak. Geometri paralel parketme konusunda bizi ışık tutacak. Nasıl mı? İşte formülü.

Bu hesaplama için bir kaç değere ihtiyacımız var:

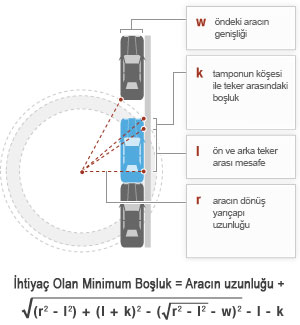
1. Aracın dönüş yarı çapı, buna r diyelim.

2. Ön ve arka teker arası mesafe ki bu l olsun.

3. Ön tamponla ön teker arası mesafe, buna da k diyelim.

4. Arkasına park etmeye çalıştığınız arabanın genişliği, bu da w olsun.

Bu değerlerin tam olarak nereler olduğunu anlayabilmek için aşağıdaki resmi de inceleyebilirsiniz.

Şimdi bu değerleri kabiliyetli bir formül içerisinde kullanalım (illüzyona bakın şimdi) ve bu noktadan sonra artık siz de mükemmel park etmeyi öğrenmiş olun.

Mükemmel paralel park etme formülü Londra Üniversitesi matematik profesörlerinden Simon Blackburn'ün çalışması. Stanford'dan başka bir matematikçi olan profesör Keith Devlin "bu formül gerçek anlamda basit matematik kullanılarak zekice hazırlanmış bir çalışma" diyor.

Devlin'in dediğine göre bir çok karmaşık parçası eski dost Pisagor teoreminin bir parçası. a kare artı b kare eşittir c kareye; bunu geometri derslerinden hatırlayamayanız yoktur şüphesiz.

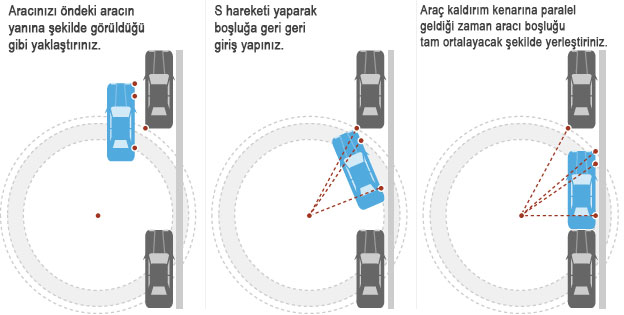
"Bu formül tam olarak ne kadar ekstra boşluğa ihtiyacınız olduğunu söylemekle kalmıyor, sadece aracınızın uzunluğuna bağımlı olmadan basit park etmenin aşamalarını da anlatıyor. Geri geri giriş yap, tekerleri düzelt ve motoru kapat." şeklinde açıklıyor Devlin.

Blackburn formülü, Pisagor'un sevilen dik açılı üçgenlerini oluşturmak için çemberin merkezini kullanır, daha sonra tam bir daire içine aracınızın dönüm yeteneğinin kavis çizimini yapar.

Bu konudaki bir çok çalışma size kolay park etmek için sadece yeterli boşluğun olması gerektiğini anlatır lakin o alana nasıl park edeceğinizi anlatmaz. Bu da çoğu insanın öncelikle "acaba yeterli alan varmı ki?" düşüncesiyle denemeler yapmasının yolunu açar ki bu işi daha da zorlaştıran bir girişimdir aslında. Devlin, tüm bu tahmin girişimlerinin arkasında işin başında matematiğin olduğunun görüleceğini söylüyor. "Matematik size insanların bir işin detaylarını anlaman için yaptığı pratiklerini ve uzmanlık girişimlerini anlamak için basit bir yol gösterir" diyor.

"Aslında, biz bir şeyin pratiğini yapmaya başladığımızda ki bu şey atletik/sportif bir şey olabilir veya otomobil olabilir fark etmez, o an için mükemmel matematikçiler olabiliyoruz ve onu organize etmek için mükemmeli arıyoruz" diyen Devlin "Fakat genellikle buna matematik olarak adlandırmayız ve tabii ki birisi arabasını mükemmel park ediyor diye matematik testinden geçer not aldın demeyiz."